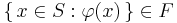Filter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in topology whence they originate. The dual notion of a filter is an ideal.
Filters were introduced by Henri Cartan in 1937[1][2] and subsequently used by Bourbaki in their book Topologie Générale as an alternative to the similar notion of a net developed in 1922 by E. H. Moore and H. L. Smith.
Contents |
General definition
A non-empty subset F of a partially ordered set (P,≤) is a filter if the following conditions hold:
- For every x, y in F, there is some element z in F, such that z ≤ x and z ≤ y. (F is a filter base)
- For every x in F and y in P, x ≤ y implies that y is in F. (F is an upper set)
- A filter is proper if it is not equal to the whole set P. This is sometimes omitted from the definition of a filter.
While the above definition is the most general way to define a filter for arbitrary posets, it was originally defined for lattices only. In this case, the above definition can be characterized by the following equivalent statement: A non-empty subset F of a lattice (P,≤) is a filter, if and only if it is an upper set that is closed under finite meets (infima), i.e., for all x, y in F, we find that x ∧ y is also in F.
The smallest filter that contains a given element p is a principal filter and p is a principal element in this situation. The principal filter for p is just given by the set {x in P | p ≤ x} and is denoted by prefixing p with an upward arrow: 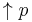 .
.
The dual notion of a filter, i.e. the concept obtained by reversing all ≤ and exchanging ∧ with ∨, is ideal. Because of this duality, the discussion of filters usually boils down to the discussion of ideals. Hence, most additional information on this topic (including the definition of maximal filters and prime filters) is to be found in the article on ideals. There is a separate article on ultrafilters.
Filter on a set
A special case of a filter is a filter defined on a set. Given a set S, a partial ordering ⊆ can be defined on the powerset P(S) by subset inclusion, turning (P(S),⊆) into a lattice. Define a filter F on S as a subset of P(S) with the following properties:
- S is in F. (F is non-empty)
- The empty set is not in F. (F is proper)
- If A and B are in F, then so is their intersection. (F is closed under finite meets)
- If A is in F and A is a subset of B, then B is in F, for all subsets B of S. (F is an upper set)
The first three properties imply that a filter on a set has the finite intersection property. Note that with this definition, a filter on a set is indeed a filter; in fact, it is a proper filter. Because of this, sometimes this is called a proper filter on a set; however, as long as the set context is clear, the shorter name is sufficient.
A filter base (or filter basis) is a subset B of P(S) with the following properties:
- The intersection of any two sets of B contains a set of B
- B is non-empty and the empty set is not in B
Given a filter base B, one may obtain a (proper) filter by including all sets of P(S) which contain a set of B. The resulting filter is said to be generated by or spanned by filter base B. Every filter is a fortiori a filter base, so the process of passing from filter base to filter may be viewed as a sort of completion.
If B and C are two filter bases on S, one says C is finer than B (or that C is a refinement of B) if for each B0 ∈ B, there is a C0 ∈ C such that C0 ⊆ B0.
- For filter bases B and C, if B is finer than C and C is finer than B, then B and C are said to be equivalent filter bases. Two filter bases are equivalent if and only if the filters they generate are equal.
- For filter bases A, B, and C, if A is finer than B and B is finer than C then A is finer than C. Thus the refinement relation is a preorder on the set of filter bases, and the passage from filter base to filter is an instance of passing from a preordering to the associated partial ordering.
Given a subset T of P(S) we can ask whether there exists a smallest filter F containing T. Such a filter exists if and only if the finite intersection of subsets of T is non-empty. We call T a subbase of F and say F is generated by T. F can be constructed by taking all finite intersections of T which is then filter base for F.
Examples
- Let S be a nonempty set and C be a nonempty subset. Then
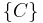 is a filter base. The filter it generates (i.e., the collection of all subsets containing C) is called the principal filter generated by C.
is a filter base. The filter it generates (i.e., the collection of all subsets containing C) is called the principal filter generated by C.
- A filter is said to be a free filter if the intersection of all of its members is empty. A principal filter is not free. Since the intersection of any finite number of members of a filter is also a member, no filter on a finite set is free, and indeed is the principal filter generated by the common intersection of all of its members. A nonprincipal filter on an infinite set is not necessarily free.
- The Fréchet filter on an infinite set S is the set of all subsets of S that have finite complement. The Fréchet filter is free, and it is contained in every free filter on S.
- A uniform structure on a set X is (in particular) a filter on X×X.
- A filter in a poset can be created using the Rasiowa-Sikorski lemma, often used in forcing.
- The set
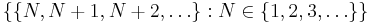 is called a filter base of tails of the sequence of natural numbers
is called a filter base of tails of the sequence of natural numbers 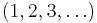 . A filter base of tails can be made of any net
. A filter base of tails can be made of any net 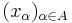 using the construction
using the construction 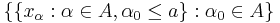 . Therefore, all nets generate a filter base (and therefore a filter). Since all sequences are nets, this holds for sequences as well.
. Therefore, all nets generate a filter base (and therefore a filter). Since all sequences are nets, this holds for sequences as well.
Filters in model theory
For any filter F on a set S, the set function defined by
is finitely additive — a "measure" if that term is construed rather loosely. Therefore the statement
can be considered somewhat analogous to the statement that φ holds "almost everywhere". That interpretation of membership in a filter is used (for motivation, although it is not needed for actual proofs) in the theory of ultraproducts in model theory, a branch of mathematical logic.
Filters in topology
In topology and analysis, filters are used to define convergence in a manner similar to the role of sequences in a metric space.
In topology and related areas of mathematics, a filter is a generalization of a net. Both nets and filters provide very general contexts to unify the various notions of limit to arbitrary topological spaces.
A sequence is usually indexed by the natural numbers, which are a totally ordered set. Thus, limits in first-countable spaces can be described by sequences. However, if the space is not first-countable, nets or filters must be used. Nets generalize the notion of a sequence by requiring the index set simply be a directed set. Filters can be thought of as sets built from multiple nets. Therefore, both the limit of a filter and the limit of a net is conceptually the same as the limit of a sequence.
Neighbourhood bases
Let X be a topological space and x a point of X.
- Take Nx to be the neighbourhood filter at point x for X. This means that Nx is the set of all topological neighbourhoods of the point x. It can be verified that Nx is a filter. A neighbourhood system is another name for a neighbourhood filter.
- To say that N is a neighbourhood base at x for X means that for all V0 ∈ Nx, there exists a N0 ∈ N such that N0 ⊆ V0. Note that every neighbourhood base at x is a filter base that generates the neighbourhood filter at x.
Convergent filter bases
Let X be a topological space and x a point of X.
- To say that a filter base B converges to x, denoted B → x, means that for every neighbourhood U of x, there is a B0 ∈ B such that B0 ⊆ U. In this case, x is called a limit of B and B is called a convergent filter base.
- For every neighbourhood base N of x, N → x.
- If N is a neighbourhood base at x and C is a filter base on X, then C → x if and only if C is finer than N.
- For Y ⊆ X, to say that p is a limit point of Y in X means that for each neighborhood U of p in X, U∩(Y − {p})≠∅.
- For Y ⊆ X, p is a limit point of Y in X if and only if there exists a filter base B on Y − {p} such that B → p.
- For Y ⊆ X, the following are equivalent:
- (i) There exists a filter base F whose elements are all contained in Y such that F → x.
- (ii) There exists a filter F such that Y is an element of F and F → x.
- (iii) The point x lies in the closure of Y.
Indeed:
(i) implies (ii): if F is a filter base satisfying the properties of (i), then the filter associated to F satisfies the properties of (ii).
(ii) implies (iii): if U is any open neighborhood of x then by the definition of convergence U is an element of F; since also Y is an element of F, U and Y have nonempty intersection.
(iii) implies (i): Define 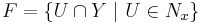 . Then F is a filter base satisfying the properties of (i).
. Then F is a filter base satisfying the properties of (i).
Clustering
Let X be a topological space and x a point of X.
- To say that x is a cluster point for a filter base B on X means that for each B0 ∈ B and for each neighbourhood U of x in X, B0∩U≠∅. In this case, B is said to cluster at point x.
- For filter bases B and C such that C is finer than B and C clusters at point x, B clusters at x, too.
- For filter base B such that B → x, the limit x is a cluster point.
- For filter base B with cluster point x, it is not the case that x is necessarily a limit.
- For a filter base B that clusters at point x, there is a filter base C that is finer than filter base B that converges to x.
- For a filter base B, the set ∩{cl(B0) : B0∈B} is the set of all cluster points of B (note: cl(B0) is the closure of B0). Assume that T is a partially ordered set.
- The limit inferior of B is the infimum of the set of all cluster points of B.
- The limit superior of B is the supremum of the set of all cluster points of B.
- B is a convergent filter base if and only if its limit inferior and limit superior agree; in this case, the value on which they agree is the limit of the filter base.
Properties of a topological space
Let X be a topological space.
- X is a Hausdorff space if and only if every filter base on X has at most one limit.
- X is compact if and only if every filter base on X clusters.
- X is compact if and only if every filter base on X is a subset of a convergent filter base.
- X is compact if and only if every ultrafilter on X converges.
Functions on topological spaces
Let E, X, Y be topological spaces with 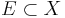 . Let B be a filter base on E and
. Let B be a filter base on E and 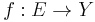 be a function. The image of B under f is f[B] is the set
be a function. The image of B under f is f[B] is the set 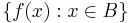 . The image f[B] forms a filter base on Y.
. The image f[B] forms a filter base on Y.
- f is continuous at x if and only if
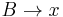 implies
implies ![f[B] \to f(x)](/2012-wikipedia_en_all_nopic_01_2012/I/9f09f6f34f7279ec8f8b60d2b9808f23.png) .
.
Cauchy filters
Let 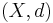 be a metric space.
be a metric space.
- To say that a filter base B on X is Cauchy means that for each real number ε>0, there is a B0 ∈ B such that the metric diameter of B0 is less than ε.
- Take (xn) to be a sequence in metric space X. (xn) is a Cauchy sequence if and only if the filter base {{xN,xN+1,...} : N ∈ {1,2,3,...} } is Cauchy.
More generally, given a uniform space X, a filter F on X is called Cauchy filter if for every entourage U there is an A ∈ F with (x,y) ∈ U for all x,y ∈ A. In a metric space this agrees with the previous definition. X is said to be complete if every Cauchy filter converges. Conversely, on a uniform space every convergent filter is a Cauchy filter. Moreover, every cluster point of a Cauchy filter is a limit point.
A compact uniform space is complete: on a compact space each filter has a cluster point, and if the filter is Cauchy, such a cluster point is a limit point. Further, a uniformity is compact if and only if it is complete and totally bounded.
Most generally, a Cauchy space is a set equipped with a class of filters declared to be Cauchy. These are required to have the following properties:
- for each x in X, the ultrafilter at x, U(x), is Cauchy.
- if F is a Cauchy filter, and F is a subset of a filter G, then G is Cauchy.
- if F and G are Cauchy filters and each member of F intersects each member of G, then F ∩ G is Cauchy.
The Cauchy filters on a uniform space have these properties, so every uniform space (hence every metric space) defines a Cauchy space.
See also
Notes
References
- Nicolas Bourbaki, General Topology (Topologie Générale), ISBN 0-387-19374-X (Ch. 1-4): Provides a good reference for filters in general topology (Chapter I) and for Cauchy filters in uniform spaces (Chapter II)
- Stephen Willard, General Topology, (1970) Addison-Wesley Publishing Company, Reading Massachusetts. (Provides an introductory review of filters in topology.)
- David MacIver, Filters in Analysis and Topology (2004) (Provides an introductory review of filters in topology and in metric spaces.)
- Burris, Stanley N., and H.P. Sankappanavar, H. P., 1981. A Course in Universal Algebra. Springer-Verlag. ISBN 3-540-90578-2.